Hephaestus Audio

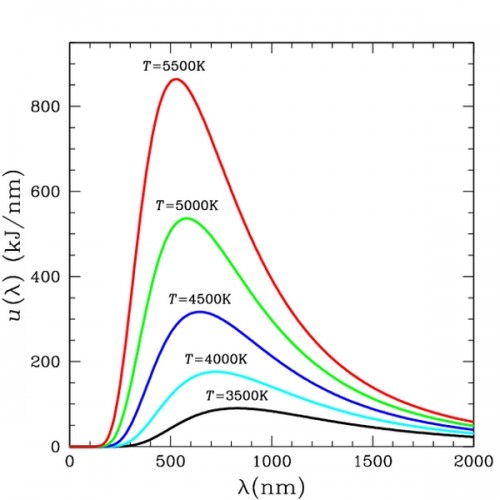
Please forgive the bitter tone that follows in this post, but recently I came across an “audiophile” device that I feel may damage the already precarious position of the audiophile industry.  First however a little necessary physics background…

A “Blackbody” is an object that does not reflect electromagnetic energy incident upon it, or allow any to pass through it.  Any emission from it is entirely thermal in nature with no characteristic emission/absorption lines from any element.  This is referred to as “Blackbody Radiation”.  Classical theory describes this spectrum with the Rayleigh-Jeans Law:

$$I(\lambda ,T)=\frac{2\pi ckT}{\lambda ^{4}}$$

$$I(\lambda ,T)$$ is the power per unit area
$$c$$ is the speed of light
$$k$$ is Boltzmann’s constant
$$T$$ is the temperature in Kelvin
$$\lambda$$ is the wavelength

This is in agreement with observation at lower frequencies, however the problem with this result is that at higher frequencies (i.e. as $$\lambda \to 0$$) the power approaches infinity!  This is certainly not in agreement with observation and has been referred to as the “ultraviolet catastrophe”.

A physicist by the name of Max Plank made an amazing assumption that was to prove instrumental not only for resolving the paradox of the Rayleigh-Jeans law, but for all of quantum mechanics.  The assumption is that radiation can only only assume discrete energy values:

$$E_{n}=nhf$$

$$n$$ is the energy level
$$h$$ is Planck’s constant
$$f$$ is the frequency.

Therefore the energy between two adjacent energy states is given by:

$$E=hf$$

The power per unit area spectrum that results from this important assumption agrees with observation and is given by the following expression:

$$I(\lambda ,T)=\frac{2\pi hc^{2}}{\lambda ^{5}(exp(\frac{hc}{\lambda kT})-1)}$$

Now I return to the bitter part of my post.  As I make clear in my Engineering Perspective article, I am not a big fan of overpriced audio interconnects.  I am not saying there isn’t a subjective improvement, but that it may not provide the greatest benefit to cost ratio for the audiophile.

However, at least these overpriced interconnects are functional.  At worst, they get the signal from point A to point B.  Even something as esoteric as a special wooden volume knob that improves your sound at least allows you to turn up the volume!  But a product that claims to dramatically improve your system by acting as an electromagnetic blackbody for your equipment is a complete waste.

There are people in this world with incredible perception that can detect “impossible” subtleties.  The purpose of the audiophile industry is to cater to these individuals – those for whom minute differences matter.  Please try to give these gifted individuals the audio experience they deserve and not just another piece of junk backed up with horrible pseudoscience.

“I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of Science, whatever the matter may be.” – Lord Kelvin

I do not completely agree with Lord Kelvin’s assertion, but there is no doubt that you must understand a subject really, really well in order to translate it into the language of mathematics.  Once you have done so however, a whole world of tools opens up.  Not only the vast array analytical tools of past generations, but the powerful simulation tools of the present.  The Calculus of Variations is one such tool – one that allows you to determine what is optimum, whether in terms of cost, time, quality, etc.

Please refer to this article for more background on the Calculus of Variations, as well as the derivation of the Euler-Lagrange Equation.

Linearity is the exception rather than the norm.  We live in a very nonlinear world – for example, it is now known that a sinusoidally driven resistor/diode/inductor combination can exhibit chaotic behavior!  Please refer to this excellent SPS Report.

One of the simplest equations that demonstrates this nonlinear behavior – this chaos – is the “Discrete Logistic Equation” or the “Logistic Map“.  Mathematically, it is given by:

$$x_{k+1}=rx_{k}\left(1-x_{k}\right)$$

This is typically used as a simple model of population growth with finite resources (i.e. food).  $$x_{k+1}$$ represents the population at the next time step, based on that at the previous time step $$x_{k}$$ where $$0\leq x_{k}\leq 1$$ with “growth rate” $$r$$ where $$0\leq r\leq 4$$.  A plot of the logistic map with respect to growth rate is given below for the interval $$2.4\leq r\leq 4.0$$:

Using MATLAB, more sophisticated visualization is possible that may give greater insight into what is happening to the population dynamics as the growth parameter is varied.  For example, how the periodic regions return to chaos via a period-doubling bifurcation.  Shown below is the interval $$3.5\leq r\leq 4.0$$: 

One lesson to take from all this with respect to audio electronics is that simplicity is best!  If a resistor/diode/inductor can result in chaos, then what can the circuitry in an overly complicated amplifier do?  Not only in electronics is simplicity the best, for example in Strunk and White’s The Elements of Style there is the simple mantra: “Omit needless words!”  Vastly different disciplines – same guiding principle.

Hamiltonian mechanics is an elegant way of formulating problems is classical mechanics.  Also, it provides insight into the world of quantum mechanics, as is evident with the Schrodinger equation.

The basic equations:

$$\dot{q}=\frac{\partial }{\partial p}H$$

$$\dot{p}=-\frac{\partial }{\partial q}H$$

Where $$q=q(t)$$ are the generalized coordinates and $$p=p(t)$$ are the generalized momenta.  H is the Hamiltonian and represents the total energy of the closed system (i.e. conservative) under consideration.  $$H=T+V$$ where T is the kinetic energy and V is the potential energy.  Also note that $$\dot{q}$$ represents the time derivative of the position, or the velocity, and that $$\dot{p}$$ represents the time derivative of the momentum, or the force.

These two equations yield the evolution of the mechanical system.  Aesthetically they are quite pleasing, owing to their nearly perfect symmetry.

Every once in a while it is important to take those dusty tomes down off the top shelf, or out of those boxes behind the furnace in the basement, and remind ourselves exactly what makes all this stuff tick.  Periodically I plan to post a little something about these fundamentals – “Physics Friday”.

This Friday the topic is one that is crucial for electronics: Maxwell’s equations.  There are a few different ways of presenting these equations, the most common one is in integral form.  This is a great form for introducing the topic, but there are only a handful of highly symmetric problems that you can attack with this.  The next most common is in differential form using the del operator with either the dot product or cross product.  This is a very useful form, although it only holds for Cartesian coordinates, which is rarely the coordinate system of choice for E&M problems.  Another differential form uses the “div” and “curl” operators, which are not only coordinate system independent, they are also very intuitive.  The “div” operator is just that – a diverging field (one that tends to move outward to infinity) and the “curl” operator is a curling field (think of the “right hand rule“).

$$div\mathbf{E}=\frac{\rho }{\varepsilon_{0}}$$

A charge density produces a diverging electric field (Gauss’s Law).

$$div\mathbf{B}=0$$

No magnetic monopoles means there is no diverging magnetic field (Gauss’s law for magnetism).

$$curl\mathbf{E}=-\frac{\partial }{\partial t}\mathbf{B}$$

A time-varying magnetic field generates a curling electric field that tends to oppose it (Faraday’s Law).

$$curl\mathbf{B}=\mu _{0}\mathbf{J}+\mu _{0}\varepsilon _{0}\frac{\partial }{\partial t}\mathbf{E}$$

A curling magnetic field is generated by either a current density or a time-varying electric field (Ampere’s Law).