“I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of Science, whatever the matter may be.” – Lord Kelvin
I do not completely agree with Lord Kelvin’s assertion, but there is no doubt that you must understand a subject really, really well in order to translate it into the language of mathematics. Once you have done so however, a whole world of tools opens up. Not only the vast array analytical tools of past generations, but the powerful simulation tools of the present. The Calculus of Variations is one such tool – one that allows you to determine what is optimum, whether in terms of cost, time, quality, etc.
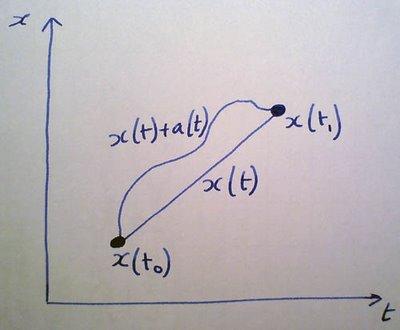
Please refer to this article for more background on the Calculus of Variations, as well as the derivation of the Euler-Lagrange Equation.
July 16th, 2009 at 1:26 pm
“Mr. Morris. That is a minus 10. Bring that calculator to me now.” James Chatfield 1992
July 16th, 2009 at 1:56 pm
“Mr. Morris, better make that a minus 20. Myes.”